71.【答案】D。解析：我们把“5对夫妇恰好都被安排在一起相邻而坐”记作事件A，由概率的定义可知，事件A的概率=事件A的情况数÷总的情况数。因此此题重点在于求事件A的情况数和总情况数。

　　10个人被安排在圆桌就餐，说明是一个环形排列问题，根据环形排列的公式可知，这10个人坐在一张圆桌的情况数为。同理，5对夫妇坐在一张圆桌的情况数为，又由于每对夫妇内部存在2种排序方式，因此事件A的情况数为×25。

　　因此事件A的概率为===，在1‰到5‰之间。因此选择D。

　　背景链接 n个物体排成一圈，有种不同的排列方式。

　　72.【答案】B。解析：根据进口价格=进口金额÷进口量，可知要求2011年货物的进口价格，则需要找到2011年货物的进口金额和进口量。由于2010年只给出了进口价格这一个量，无法计算2011年的进口金额和进口量，因此需要利用特值法进行适当的假设。

　　设2010年的进口量为1公斤，则2010年的进口金额为15×1=15元。

　　由于2011年进口量增加了一半，进口金额增加了20%，则2011年进口量为1×(1+)=1.5公斤，进口金额为15×(1+20%)=18元。

　　2011年进口价格=进口金额÷进口量=18÷1.5=12元/公斤，因此选择B。

　　73.【答案】D。解析：假设A等有x幅，B等有y幅，C等有z幅。可列出方程组为：

　　此题其实可以根据z-x=5，推算出三组解或者或者。可排除掉A、B、C。

　　74.【答案】B。解析：已知花坛是半径为10米的大圆，喷头是半径为5米的小圆，此题转化为求“多少个半径为的小圆可以完半径为r的大圆?”首先4个小圆的面积和恰好等于一个大圆的面积。为小圆尽可能的覆盖大圆，当4个小圆不重叠时，所覆盖大圆部分的面积必小于大圆自身面积。若用5个小圆覆盖大圆，因为小圆的直径等于大圆的半径，所以当5个小圆不重叠时，无法盖住大圆的圆周，而6个小圆则恰好盖住大圆圆周，此时中间空白处再加1个小圆，可将大圆完，所以共需要7个小圆。如图所示：

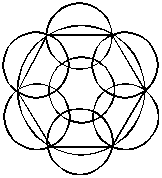
　　故此题选择B。

　　75.【答案】C。解析：设乙每小时走的路程为1，追及距离为1×2=2。甲跑半小时休息半小时，跑步的半小时追上(2.5-1)×0.5=0.75的距离，休息的半小时又拉开了0.5。

　　每小时甲实际可追上0.75-0.5=0.25，2=0.25×5+0.75，甲在前5个小时追上1.25的距离，最后0.75的距离正好需要花半个小时追上。一共需要5个半小时，即14∶30分追上。选择C。

　　另解在不愿意计算的情况下，可直接列表将每个小时二者的路程标出来，这样无需计算可得出答案。甲半个小时走2.5×0.5=1.25，乙每半小时走0.5。

　　正好在14∶30追上乙。利用表格来做的话，不容易出错。

　　76.【答案】A。解析：相同时间内，A、B、C三队分别完成了自己任务的90%、50%和50%×80%=40%，即他们的工作量之比为9∶5∶4，故他们的工作效率之比为9∶5∶4。不妨设他们的效率分别为9、5、4。

　　A队派出的人力加入C队以后，A队的工作效率减少了9×=6，变为9-6=3，C队的工作效率变为4+6=10。

　　A队还剩下10%的任务，需要10%÷3=3.33%的时间，C队还剩下60%的任务，需要60%÷10=6%的时间。可见C队后完成任务，此时B队又完成了6%×5=30%的任务，故B队一共完成了50%+30%=80%的任务。选择A。

　　77.【答案】D。解析：此题条件比较单一，没有直接可利用的数量关系。因此，考虑方程法，利用方程来理清数量间的特殊关系。

　　设大包装盒有x个，小包装盒有y个，则12x+5y=99，其中x、y之和为十多个。对于这个不定方程，从整除特性等方面来考虑没有思路。但是我们注意到：

　　5y的尾数只能是5、0，那么对应的12x的尾数只能为4或者9，而12x为偶数，故尾数只能为4。此时，只有x=2或者x=7时满足这一条件。

　　当x=2时，y=15，x+y=17，正好满足条件，y-x=13;

　　当x=7时，y=3，x+y=10，不符合条件。

　　综上所述，只能选择D。

　　78.【答案】B。解析：题中的关键词在于“等差数列”和“平均数”。等差数列的平均数与其等差中项有关系。

　　9人的得分构成等差数列且平均分是86分，则该数列的等差中项，即第5名工人得分为86分。同理，前5名工人得分之和为460，则其等差中项第3名得分为460÷5=92分。可知第4名得分为(92+86)÷2=89，前7名得分之和为89×7=623，选B。

　　79.【答案】C。解析：旗杆的高度为5，最小为1。因此这两个旗杆间的距离不超过(5-1)×10=40米。考虑其余旗杆的位置分布，设任意旗杆高度为x。要满足与1米旗杆间距离不超过它们高度差的10倍，应在下图左边的圆范围内。要满足与5米旗杆间距离不超过它们高度差的10倍，应在下图右边的圆范围内。同时满足条件的旗杆只能位于两个旗杆的连线上。所以满足条件的旗杆都位于一条直线上，最少需要40×2=80米即可把它们都围进去。

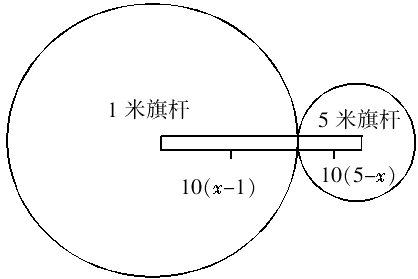
　　80.【答案】C。解析：正八面体的体积公式没有学过，但由图中可以看出，将正八面体拆解为两个完全相同的四棱锥，而每个棱锥的体积V=Sh，高度h正好为正方体边长的一半，即3厘米，现在只需要求棱锥的底面积S。

　　将棱锥的底面单独拿出来看，如下图所示：

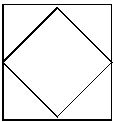
　　棱锥底面积正好等于正方体底面积的一半，即为6×6÷2=18平方厘米。因此每个棱锥的体积为×18×3=18立方厘米，正八面体体积为18×2=36立方厘米。因此选择C。

（责任编辑：李明）